Lesson 1: Rates of Change
Unit 1: Rates of Change
- change over an interval and instantaneous rate of change at a point, using the slopes of secants and tangents and the concept of the limit;
- between the numeric, graphical, and algebraic representations of a function and its derivative;
- graphically and algebraically the rules for determining derivatives; apply these rules to determine the derivatives of polynomial, sinusoidal, exponential, rational, and radical functions, and simple combinations of functions; and solve related problems.
Lesson 1: Rates of Change
Refresh Your memory – Review
Following are some topics you will need to know to start this course. If you are NOT comfortable with these topics, you need to revisit them or take a pre-requisite foundation math course prior to continuing.
- Factoring Trinomials
Difference of squares
Sum of Cubes
Difference of Cubes
Factor Theorem: A polynomial P(x) has a factor x – a if and only if P(a) = 0.
EXAMPLE:
Rationalizing a Denominator
- the process of changing a denominator form a radical (square root) to a rational number (integer)
- reason that we rationalize denominators is that dividing by an integer is preferable to dividing by a radical number.
Note: when the denominator of a radical fraction is a two term expression, you can rationalize the denominator of by multiplying the conjugate.
EXAMPLE:
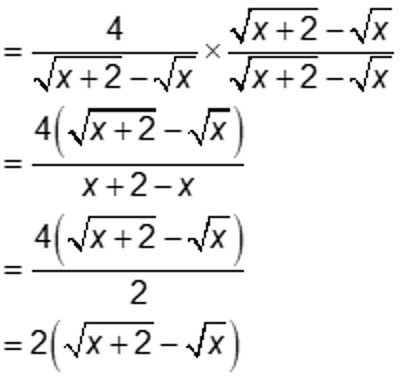
2. Linear Functions
- a linear function is a function of the form
or
, where m = slope, b = y-int of the line
- the slope of a line that passes through the points P1(x1, y1) and P2(x2, y2) is defined by
- since the slope is the ratio of the change in y to the change in x, it can be interpreted as the “rate of change of y with respect to x”.
- Sequences and Series (covered in Grade 11 U and M Mathematics)
- Slope of the Tangent, Slope of the Secant, Slope of the Tangent at an Arbitrary Point
A tangent is the straight line that most resembles the graph near a point. Its shape tells how steep the graph is at the pint of tangency. In the figure below, four tangents have been drawn.
To determine the equation of a tangent to a curve at a given point, we fist need to know the slope of the tangent. When only one point is known, proceed as follows;
Consider a curvy y=f(x) and a point P that lies on the curve. Now condister another point Q on the curve. The ling joining P and Q is called a secant. Think of Q as a moving point that slides along the curve towards P, so that the slope of the secant PQ becomes a progressively better estimate of the slope of the tangent at P.
Therefore, the definition for the slope of the tangent might be;
The slope of the tangent to a curve at a point P is the limiting slope of the secant PQ as the point Q slides along the curve towards P. In other words, the slope of the tangent is said to be the limit of the slope of the secant as Q approaches P along the curve.
The slope of the tangent to the graph y=f(x) at point P(a, f(a)), is
Rates of Change
Recall the slope of a line. Since the slope is the ratio of the change in y to the change in x, it can be interpreted as the rate of change of y with respect to x.
Below are real-world examples of rates of change.
EXAMPLE 1
The boiling point is the temperature at which a liquid changes to gas. When water is heated it eventually reaches a temperature – the boiling point – at which the vapour pressure is large enough that bubbles are formed inside the body of the water. The boiling point depends on the pressure and the boiling points of water at pressures ranging from 0.5 psia to 1000 psia can be found in the diagram and table below.
Describe the rate of change that is occurring both on the pressure and the boiling points of water ranging from 0.5 psia to 1000 psia.
SOLUTION:
The rate of change on the pressure is linear since it is increasing at a constant rate. The rate of change on the boiling points is non-linear in both degrees F and degrees C because the temperature is rising at a non-constant rate.
EXAMPLE 2:
When a bathtub is draining, would you expect half of the water to drain in half of the time? Explain.
Draining Water from a Bathtub
| Time(s) | Volume(L) |
| 0 | 900 |
| 10 | 715 |
| 20 | 551 |
| 30 | 403 |
| 40 | 283 |
| 50 | 179 |
| 60 | 89 |
| 70 | 42 |
| 80 | 12 |
| 90 | 0 |
SOLUTION:
Water pressure would make the water drain quicker at the beginning than near the end of the draining process. Therefore, it would drain half of the water in less than half the time.
