Lesson 1: Uniform Motion

Download here: Ontario Curriculum Expectations

Take the first step in faith. You don’t have to see the whole staircase, just take the first step.

Dr. Martin Luther King Jr.

Motion

The speed limit on major highways in Ontario is 100 km/h. However, the speed limit on most city streets is only 50 km/h. It would seem to make sense that by increasing the speed limit, vehicles could reach their destination sooner, clearing the roads for other traffic. However, what about the safety concerns? If vehicles were moving faster, drivers would have less time to react to avoid dangerous situations. Would higher speed limits result in more traffic accidents?

The study of uniform motion looks at how far objects travel, how long they are travelling for, and how quickly they are moving.

Distance versus Displacement:

In Physics, there is a very important difference between the terms distance and displacement.

Distance is the total length of the path that an object travels. We use the symbol “∆d” to represent distance and it is measured in metres (m).
Displacement is the change in an object’s positon. It measures the straight line distance between the starting point and the end point of an object’s motion. We use the symbol “” to represent displacement and it is also measured in metres (m). Displacement always includes a direction.

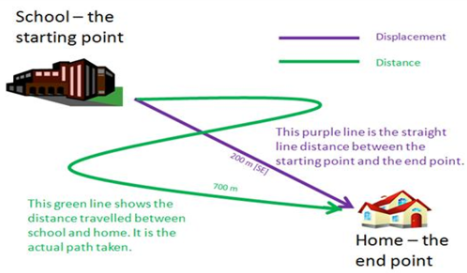
The arrow that is placed above  indicates that displacement is a vector. This means that it must have a direction. Distance is not a vector and does not include a direction. Quantities like distance that do not have a direction are called scalars.

In the above example, the distance would be 700 m and the displacement would be 200 m [SE].

Practice Questions

1. A car travels 300 m [N] along a road, then turns a corner and drives an additional 400 m [E]. Draw a vector diagram of the path travelled by the car, and then calculate the car’s distance travelled and its displacement.

Answer

Given: The car travels 300 m [N], then 400 m [E].

The black lines represent the car’s distance.

The red line represents the car’s displacement.

Required:

Δd = ?

 = ?

Solution:

∆d = the length of the path travelled

= 300 m + 400 m

= 700 m

 = the straight line distance between the starting point and the end point. It must also include a direction. You can use the Pythagorean Theorem and trigonometry ratios to solve this, however, a ruler and protractor will suffice provided you have drawn an accurate scale diagram.

 = 500 m [N53.1°E]

The car travels a distance of 700 m and has a displacement of 500 m [N53.1°E].

2. Most football fields have a 400 m running track that goes around them. If you were to run around this track once, what distance would you have run? What would your displacement be?

Answer

Running track around a football field.

Since the track is 400 m long, your distance would just be 400 m.

Displacement is the straight line distance between the starting point and end point. Since you start and end at the same point, your displacement will be 0 m.

Speed versus Velocity:

Speed is a measure of how fast we are moving. It allows us to calculate how much distance we are covering in a given amount of time. We represent speed using the lower case letter v and measure speed in metres per second (m/s).

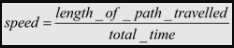
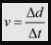
Velocity is a measure of how fast we are moving in a given direction. Like displacement, velocity is also a vector and must have a direction. We use the symbol  V to represent velocity. We measure velocity in metres per second (m/s).

velocity=displacement/time

Sample Problem 1

Michael can run 100.0 m in a time of 12.5 s. What is his speed?

Given:

Δd = 100.0 m

Δt = 12.5 s

Required:

v = ?

Solution:

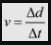
v=100m/12.5s

v = 8.0 m/s

Michael is able to run at 8.0 m/s.

Sample Problem 2: Rearranging the Equation

Leroy is able to run at a speed of 9.5 m/s. How long will it take Leroy to complete the 100.0 m race?

Given:

Δd = 100.0 m

v = 9.5 m/s

Required: Δt = ?

Solution:

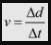
We need to arrange the equation in terms of Δt.

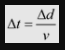
Δt = 10.5 s

Leroy can run 100.0 m in 10.5 seconds.

Practice Questions

1. Continuing from “Check Your Understanding” question 1: A car travels 300 m [N] along a road, then turns a corner and drives an additional 400 m [E]. If the entire trip took 35.0 s, calculate the car’s average speed and velocity.

Answer

Finding Speed:

Given:

Δd = 700 m

Δt = 35 s

Required:

v = ?

Solution:

v = 20 m/s

The car is travelling at a speed of 20 m/s.

Finding Velocity:

Given:

= 500 m [N53.1°E]

Δt = 35 s

Required:

= ?

Solution:

= 14.3 m/s [N53.1°E]

The car’s velocity is 14.3 m/s [N53.1°E]. Remember, velocity is a vector and therefore must have a direction.

2. Continuing from “Check Your Understanding” question 2: Calculate your speed and velocity if you were able to run around the 400 m track in 1 minute and 20 seconds.

Answer

Finding your speed as you run one lap of the track:

Given:

Δd = 400 m

Δt = 1 minute and 20 seconds. Since 1 minute = 60 seconds, Δt = 80 s.

Required:

v = ?

Solution:

v = 5 m/s

You are running at a speed of 5 m/s.

Finding your velocity as your run one lap of a track:

Given:

= 0 m

Δt = 80 s

Required:

= ?

Solution:

= 0 m/s

Your velocity is 0 m/s because you are ending at the same point as you started.

3. A tractor pulls a wagon of school children from a farmhouse to a corn field. It travels at a speed of 20 km/h for two minutes. How far is it between the farmhouse and the corn field? (Hint: You will first need to determine the speed in metres/second and the time in seconds.)

Answer

Given:

v = 20 km/h. Since 20 km = 20 000 m, and 1 h = 60 min = 3600 s, = 5.56 m/s.

Δt = 2 min = 120 s.

Required:

Δd =?

Solution:

We need to arrange the equation in terms of Δd.

Δd = vΔt

Δd = (5.56 m/s)(120 s)

Δd = 667.2 m

It is about 667 m between the farmhouse and the cornfield.