Lesson 2: Understanding Limits

By definition a limit is: A function f  has a limit L as x approaches a, written  provided that the values of f(x) get closer and closer to L as x gets closer and closer to a, on both sides of a, but x ≠ a. 

Another way to state this definition is to say that a limit is the intended height (where height f is a function in term of time x) of a function. 

Determining the height of a function 

Example 1:

This function changes height all throughout its domain.  That different “x” values have different heights. 

What is the height of the above function when x = 2? 

Solution:

The function reaches a height of 4 when x = 2.  A limit statement can be made.  which simply means that the function as x approaches 2 is getting closer to the height of 4. 

Functions that don’t reach their intended heights 

Functions that don’t reach their intended heights 

Example 2: Can a function have a limit if it can’t reach its intended height? 

This function appears to be a regular function; however, there is a hole in the middle of the line representing this function. 

When x =2 the function is undefined. 

When we substitute x = 2 into the function the following happens. 

When Does a Limit Exist? 

A limit exists if you travel along a function from the left side and from the right side towards some specific value of x. In other words, as long as the y-values from the left and right are the same then the limit exists. 

Example 3: What is the Limit of the function shown below? 

Solution:

For a limit to exist the left hand limit must equal the right hand limit. 

So, in this example the limit does not exist.  

This is also called a discontinued function.  If the limit did exist it would be called a continuous function. 

Discontinued Function:

Continuous Function:

Evaluating Limits (substitution)

Example 4:

Solution:

Substitute 3 in for n.

Therefore,

Note: If you substitute and there is an answer, the limit is the answer. 

Example 5:

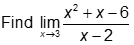
Solution:

Factor the numerator first then since a substitution yielded an undefined answer, cancel out common factors to the numerator and denominator and substitute. 

Therefore,

Example 6: Find

Solution: Conjugates are used to evaluate this question because we must rationalize the numerator (see Lesson 1).   

Therefore,