Lesson 4: Limits & Instantaneous Rates of Change Derivative

The Derivative at a Point 

Previously it was mentioned that the instantaneous rate of change at point P(a, f(a)) is equal to the slope of the tangent line at that point. 

The slope of the tangent line is the limiting value of the slopes of the secants, represented by PQ, as point Q approaches point P along the curve.   

 is the interval between the x-coordinates of P and Q.  So, = x – a or x = a + . 

The coordinate Q can be expressed as Q(a + , f(a + )) and  = f(a + ) – f(a). 

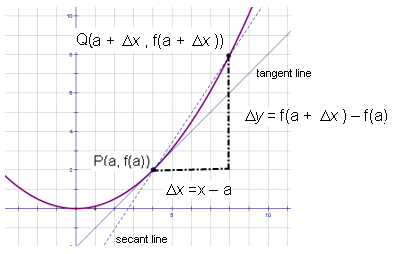
Therefore the slope of the tangent can be determined as such: 

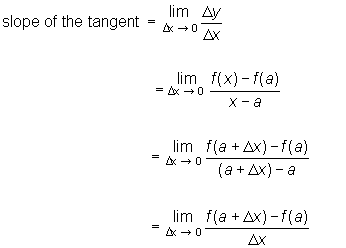
When we let h = then slope of the tangent becomes

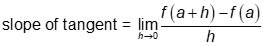
Therefore, the derivative at a point is defined as:

The derivative of a function f at point (a, f(a)) is f¹(a) = , if this limit exists.  The notation  is read “f prime of a” and is the slope of the tangent to the function . 

Example 1:

Determine the equation of the tangent to the curve defined by  at point (3, -10). 

Solution 

The derivative is used to find the slope of the tangent at ((a, f(a)) = (3, -10). 

Remember that:    so,

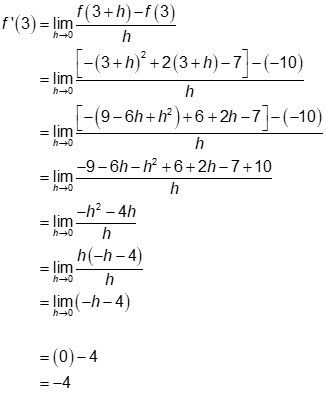
At point (3, -10), the slope of the tangent is –4.  Use y = mx + b and substitution to find the equation of the tangent. 

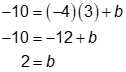
Therefore the equation of the tangent is . 

Example 2:

Sketch the graph of f(x) and the tangent line from example 1. 

Solution:

To get the points for the parabola completing the square is required.  First you must put the quadratic equation in vertex form . 

The vertex of the parabola is (1, -6) and the y –intercept is –7.